【正規分布①】
今回は、統計の世界に外すことのできない正規分布について説明する。
正規分布をもとにして、検定方法が用意されているぐらいなので、とにかく重要である。
というわけで、今回は正規分布について説明していく。
スポンサードサーチ
正規分布
正規分布$は、全体を100%(もしくは1)とみなしたときに、『ある範囲において全体の何%いるのか』ということを算出できる分布になっている。
といっても意味が分からないと思うので、とりあえず進めていく。
正規分布を式で表すと、
で表される。
$x$は確率密度変数、$\mu$は母平均、$\sigma^2$は母集団における分散、$\sigma$は標準偏差である。
ちなみに、$\exp(x) = e^x$のことである。
全然分からんって人は、以下でそれぞれ説明しているので勉強してきてくれ!
・【統計の平均・分散・標準偏差】すでに知ってるかもしれないが導出しておく
・【統計:母集団・標本】すでに知ってるかもしれないが説明しておく
そして正規分布を図で表すと以下のようになる↓
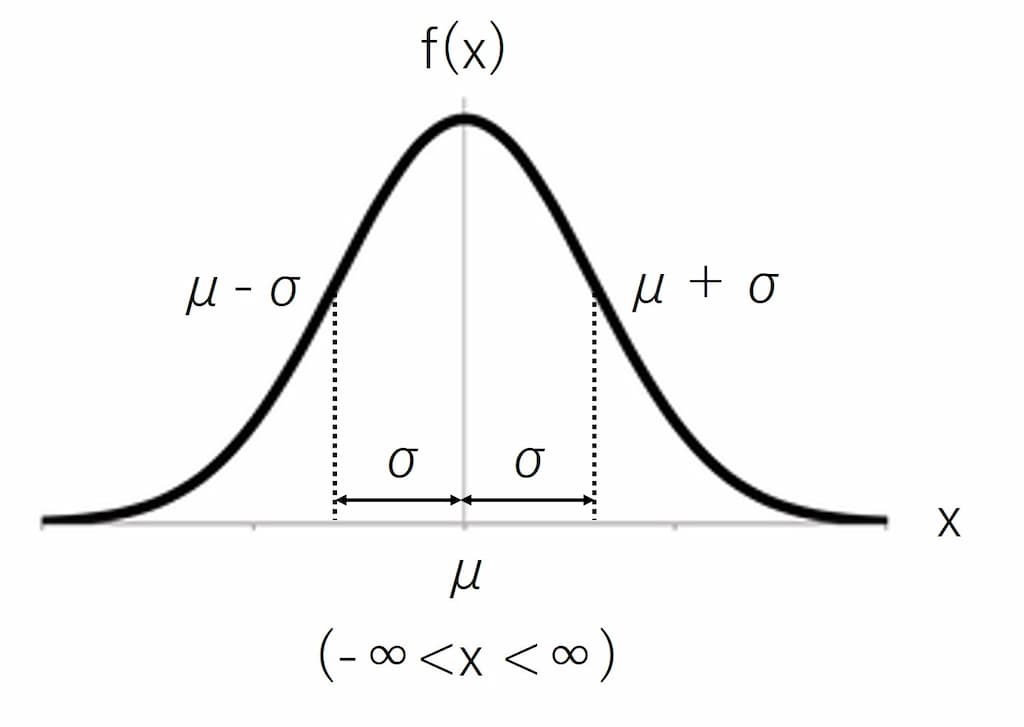
横軸は$x$、縦軸は$f(x)$であり、x軸を見ると平均である$\mu$のところに山のてっぺんが来るようなグラフになっている。
また、山のなだらかなところに標準偏差である$\pm \sigma$が来るようになっている。
さらに、最初に言ったように、このグラフ全体を足すと1(100%)になるという性質を持っている。
とりあえずは『こんなグラフなのかー』と眺めてほしい。
正規分布をどう使うんや?
で、この正規分布の式をどうするかというと、積分していく。
積分することで何割いるのかという値を出していくわけだ。ちなみにグラフ全体は1であることをお忘れなく。
例えば、$\mu-\sigma ~\mu+\sigma$のように、プラスマイナス標準偏差の間で積分をかますと
$$ \int_{\mu-\sigma}^{\mu+\sigma} f(x) dx = \int_{\mu-\sigma}^{\mu+\sigma} \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{1}{2}\left(\frac{(x-\mu)}{\sigma} \right)^2\right) dx$$
と表される。
グラフにしてみると、以下のようになる。
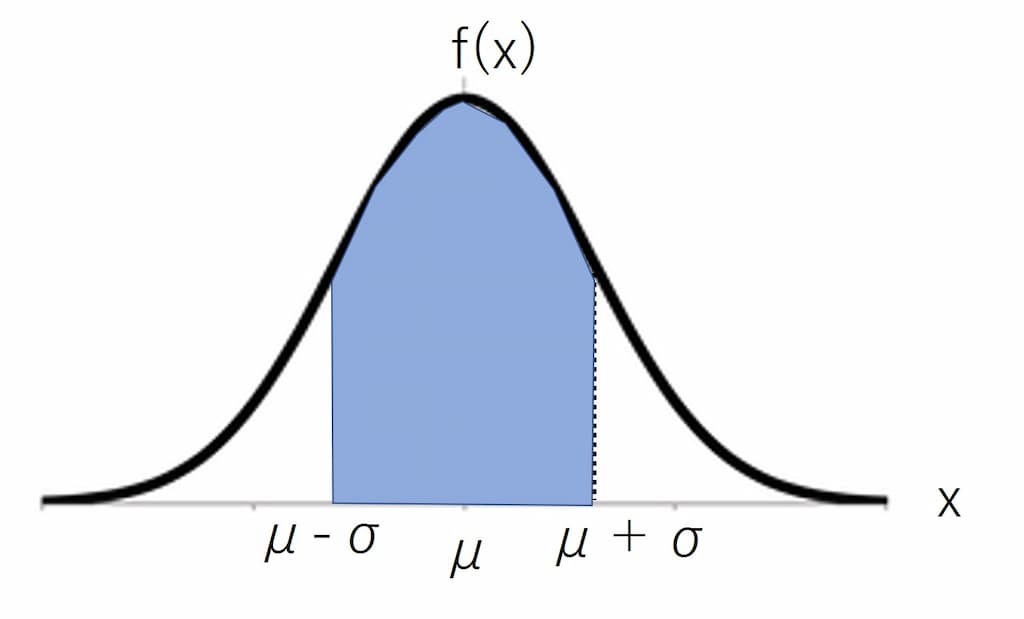
上の青い面積を求めることで、全体の何割がその範囲に入るのかということが分かるわけだ。
しかしながら、正規分布の式は積分できないし、一般的に応用するには少し工夫が必要になる。
『積分できないのにどうやって求めるんだよ…』というところは次回解説しようと思う。
まとめ
- 正規分布のグラフは、平均$\mu$の位置に山のてっぺんがきて、両側のなだらかな部分に$\pm\sigma$が来る。
- 正規分布の面積を求めることで、全体の何割がいるのか分かる
画像提供:[フリー素材] 正規分布とポアソン分布: Royality-free illustrations of statics
