2021/03/07 (更新日: 2021/03/28)

【正規分布②】すでに知っているかもしれないが説明しておく

数学

前回：【正規分布①】すでに知っているかもしれないが説明しておくの続き。

正規分布の式は積分できないので、このままでは何も求めることができない。
そこで、まずは$\mu =1,\sigma =1$の正規分布を考えてみる。この、$N(\mu ,\sigma )=N(0,1)$を標準正規分布と言う。
また、$N(\mu ,\sigma )$は正規分布を表している。

スポンサードサーチ

標準正規分布

一般の正規分布は、

だったが、ここで標準正規分布は、$\mu =0,\sigma =1$だったので、これを代入して、

となる。

で、例えば以下の範囲での面積を求めてみようと思う。

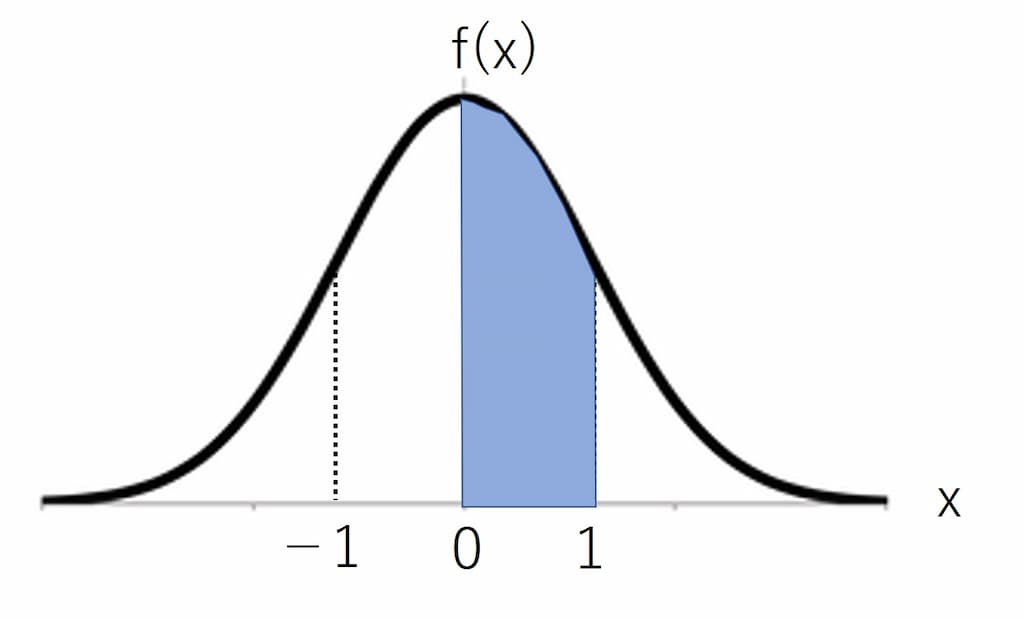
式で表すと、
$${\int }_{-1}^{+1}\frac{1}{\sqrt{2\pi }}\exp (-\frac{x^2}{2})dx$$
となる。
だが、ここまで持っていたとしても積分はできない。

正規分布表というものがあるで！

積分はできないというのは、正確には不定積分はできないということだ。
つまり、$\exp (\frac{-x^2}{2})$に関する不定積分(変数が残っている形)はできないが、定積分(具体的な数値)は求めることができる。

標準正規分布における値は既に求められており、標準正規分布表に全てが書いてある。
>> 標準正規分布表

上記リンクでは、片側のZいった分だけ求めることができる。
この場合で行くと、$Z＝0\sim 1$(このブログでいうなら$x=0\sim 1$)の面積は、0.3413になる。片側で約3.5割の面積をかカバーしていることになる。

また、$x=-1\sim +1$の範囲では、片側0.3413を2倍して0.6826になり、これだけで約7割の面積をカバーしていることになる。

標準は一般ではない

だが、ここまではあくまで$\mu =0,\sigma =1$の分布であり、世の中そんな綺麗な数字にはならない。圧倒的に$N(\mu ,\sigma )$の場合の方が多い。

そこで、一般の正規分布を$\mu \sim a$まで積分した場合を考えてみる。$a$というのは、任意の範囲で積分することを表す。

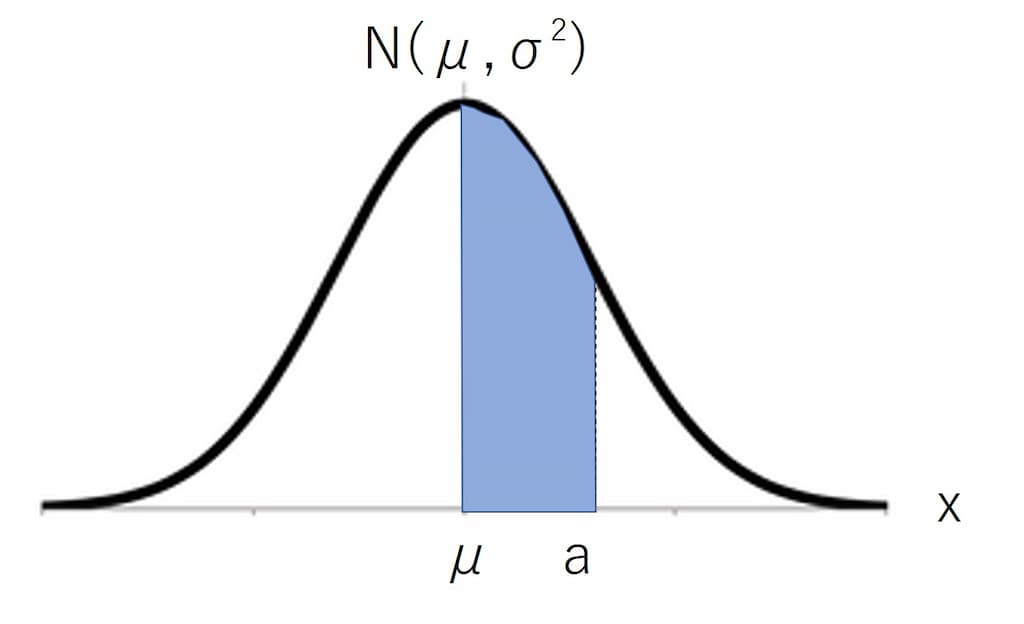
式で表すと、
$${\int }_{\mu }^a\frac{1}{\sqrt{2\pi }\sigma }\exp (-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2)dx$$

ここで$\exp$の中$\frac{x-\mu }{\sigma }$を$z$と置く。

次に$z$で積分をしようと試みる。$z$を微分すると、
$$\frac{dz}{dx}=\frac{1}{\sigma }$$
積分範囲$\mu \sim a$はそれぞれ、

よって、$Z$の範囲は$z=0\sim \frac{a-\mu }{\sigma }$となり、この範囲を積分することになる。

で結局のところ、以下のように$z$の変数に変換できる。

ここで、(★z)式は、$\mu =0,\sigma =1$の時の標準正規分布の式と同じ形をしている。

というわけで、$(★z)$式に対して、標準正規分布で使用した標準正規分布表が使える。

注意するのは範囲だけ

これで、一般の正規分布に対しても、標準正規分布表から面積(割合)を求められることが分かった。
ただ、注意すべきなのは範囲が変わるということだ。

このzにおける$\frac{x-\mu }{\sigma }$の部分を、$z$における標準化変換という。

$\mu ,\sigma$は分かっている。後は問題によってxの範囲を決めてしまえば、z求まるわけだ。

スポンサードサーチ

正規分布を使った問題

正規分布はこんな風に使うんやで、ってことで例題を解いてみよう。

(1)の解説

とりあえずこの正規分布を図で表すと以下のようになる。

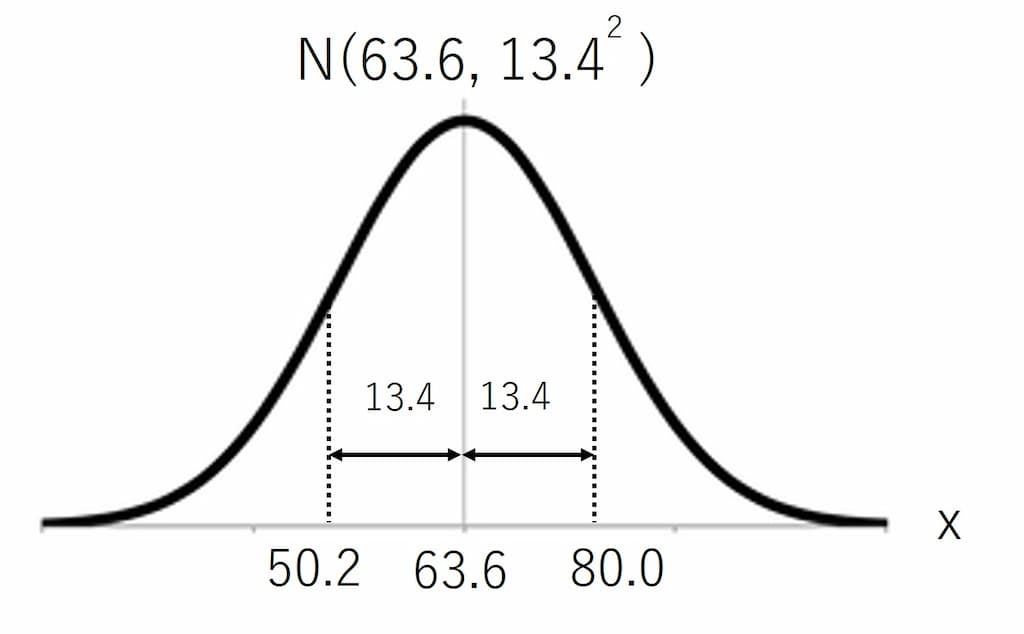
で、この試験の受験者は30000人である。
(1)の75点の人は何番かというのは、全体の数が分かっていて、75点までの割合が分かれば求まりそうだ。というわけで、標準化変換をかましていく。

$\mu =63.6,\sigma =13.4$であり、$x=75$を代入すると、$z=\frac{x-\mu }{\sigma }=\frac{75-63.6}{13.4}=0.8507\dots$となる。
ちなみに、標準正規分布表を見てみると、0.3023と分かる。

ただ、この0.3023というのは平均である63.6点から75点の範囲なので、0点から63.6点までも考慮する必要がある。
0点から63.6点までは正規分布全体のうちの半分なので0.5となる。よって、$0.5+0.3023=0.8023$となる。

求めたいことは75点の人は何位になるかということなので、$30000\times 0.8023=24069$
で、ここで求めた順位はおしりから数えたものになるので、全体から24069を引くと、5931となる。よって(1)の答えは5931番となる。

また、正規分布表から求めた値より0.0007分大きいことを考慮して、24069番より大きいと考え、24070番と治して5930番と求めてもいい。

(2)の解説

20000番目の人を考える前に、15000番目の人の点数は63.6点付近であることを思い出そう。

でちょっとややこしいのが、63.6点付近より点数が高くなると順位は小さくなるので14999以下になる。そして問題となっている『20000番目の人が何点か』ということは、平均点63.6点より低いことが分かる。そこに注意して求めてみよう。

ただ、求める割合は変わらない。20000/30000 = 0.666…となり。半分の0.5を引くと、0.166…となり、この値を標準正規分布表で逆に0.1666…に近い値を探す。すると、$z=0.43$のとき、0.1664となって近そうだ。というわけで、$z=0.43$を採用する。

標準化変換の式で、普通はzを求めるが、今回はxについて解いていく。
すると、$x=z\times \sigma +\mu =0.43\times 13.4+63.6=69.362$となる。
で、5000番目の人であればこれが答えなのだが、今求めたいのは20000番目の点数である。平均戸の差分は69.362-63.6 = 5.762点となる。よって、この平均からこの点数分低い時が20000番目に値する人なので、63.6-5.762 = 57.838点となる。で実際の点数に治すと58点となる。

だが、標準正規分布表から逆算した際に、少し小さい値を選んだため57点でも良い。

まとめ

今回は正規分布の具体的な求め方を解説した。
重要なことは標準正規分布表と標準化変換だ。とりあえず、これを覚えておけばいい思う。

統計

• facebook
• Tweet
• hatebu
• Share
• Read Later